1        加速退化试验数据统计分析方法

1.1     基于Arrhenius模型的加速退化试验数据处理

1.1.1 数据输入

阿伦尼乌斯(Arrhenius)模型适用于加速应力为温度，漂移布朗运动中的漂移系数与所施加的温度之间的关系服从

；

。

式中：A为大于0的常数，S为绝对温度(等于摄氏度加273.15)，k为波尔兹曼常数，等于，为激活能，单位为。

令，，，则。

式中：a, b为待估参数，为应力S的已知函数。

要采用阿伦尼乌斯(Arrhenius)模型进行计算，需要输入以下数据

（1）加速应力水平S₁, S₂, ..., S_k，k为加速试验组数；

（2）每种加速应力下的试验样本数n₁, n₂, ..., n_k，样本总数；

（3）每种加速应力下产品性能的检测次数m₁, m₂, ..., m_k，总检测次数；

（4）每种加速应力下产品性能的每次检测时间t_lj及检测到的性能值y_lij，其中l =1, ..., k; i = 1, ..., n_l; j = 1, ..., m_l；

（5）性能阈值（即产品性能超过时判定为失效），性能初值（可选输入，用户有输入时应用输入值，无输入时应用评估值），规定应力，规定时间。

1.1.2 评估过程

（1）由最小二乘准则下的拟合分析，得到每种加速应力下的性能退化率

；

；

；

；

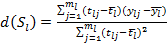（2）由数对（l = 1, ..., k）通过最小二乘准则下的拟合分析求a, b,

；

；

；

；

；

（3）若用户未输入性能初值，通过以下公式求

。

1.1.3 结果输出

；

，

其中，为标准正态分布的累计概率分布函数。

由此，可以得到产品在正常应力水平下的寿命及可靠度分布曲线，给定时间，可以输出产品的可靠度R()；或者给定可靠度R，可以输出产品的可靠寿命T_R。